Forces structured questions
2009 May-Jun Paper-41 Q3
Question (a)(i)
Fig. 3.1 shows a skier descending a hillside. Fig. 3.2 shows the speed/time graph of his motion.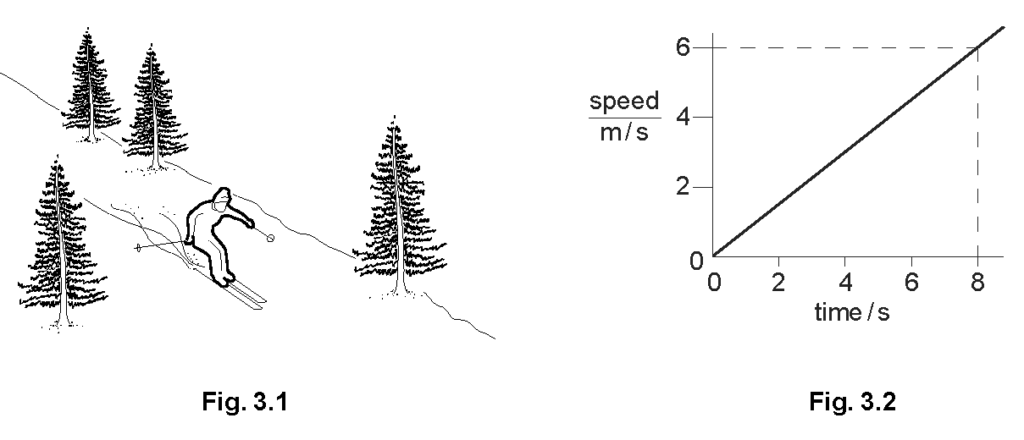 How can you tell that the acceleration of the skier is constant during the 8 s shown on the graph?
How can you tell that the acceleration of the skier is constant during the 8 s shown on the graph?
Explanation: A straight line on a speed/time graph indicates a constant acceleration.
Question (a)(ii)
Calculate the acceleration of the skier.
Explanation: The acceleration is calculated using \(a = \frac{Δv}{t} = \frac{6 \text{ m/s}}{8 \text{ s}} = 0.75 \text{ m/s}²\).
Question (b)(i)
Another skier starts from rest at the top of the slope. As his speed increases, the friction force on the skier increases. State the effect of this increasing friction force on the acceleration.
Explanation: Increasing friction force opposes the motion, reducing the acceleration.
Question (b)(ii)
Eventually, the speed of the skier becomes constant. What can be said about the friction force when the speed is constant?
Explanation: When the speed is constant, the forces are balanced, so the friction force equals the forward/downward force.
Question (b)(iii) 1.
On the axes of Fig. 3.3, sketch a possible speed/time graph for the motion of the second skier.
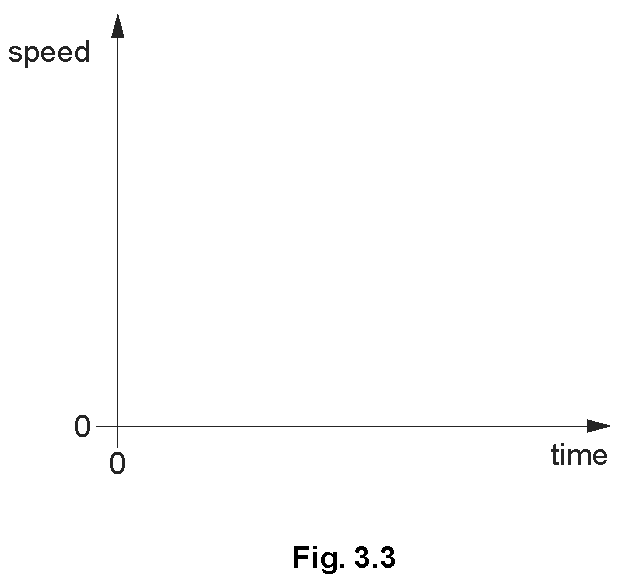
Explanation: This shape represents the skier's acceleration decreasing over time until reaching a constant speed.
Question (b)(iii) 2.
On your graph, mark with the letter A a region where the acceleration is not constant. Mark with the letter B the region where the speed is constant.
– Label B on horizontal region.
Explanation: The curved region indicates changing acceleration, and the horizontal region indicates constant speed.
2010 May-Jun Paper-41 Q3
Question (a)
Two students make the statements about acceleration that are given below.
Student A: For a given mass the acceleration of an object is proportional to the resultant force applied to the object.
Student B: For a given force the acceleration of an object is proportional to the mass of the object.
One statement is correct and one is incorrect.
Re-write the incorrect statement, making changes so that it is now correct.
For a given ______, the acceleration of an object is ______.
Explanation: The correct relationship is that acceleration is inversely proportional to mass for a given force, according to Newton's second law of motion.
Question (b)
State the equation which links acceleration \(a\), resultant force \(F\) and mass \(m\).
Explanation: This is Newton's second law of motion, stating that force equals mass times acceleration.
Question (c)(i)
Describe what happens to the motion of a moving object when there is no resultant force acting on it.
Explanation: When no resultant force acts on an object, it maintains its state of motion, according to Newton's first law of motion.
Question (c)(ii)
Describe what happens to the motion of a moving object when a resultant force is applied to it in the opposite direction to the motion.
Explanation: A force opposite to the direction of motion causes deceleration, reducing the object's speed.
Question (c)(iii)
Describe what happens to the motion of a moving object when a resultant force is applied to it in a perpendicular direction to the motion.
Explanation: A perpendicular force causes the object to change direction, resulting in a curved trajectory.
2010 May-Jun Paper-42 Q5
Question (a)
The apparatus shown in Fig. 5.1 is used to demonstrate how a coin and a piece of paper fall when they are released from rest.
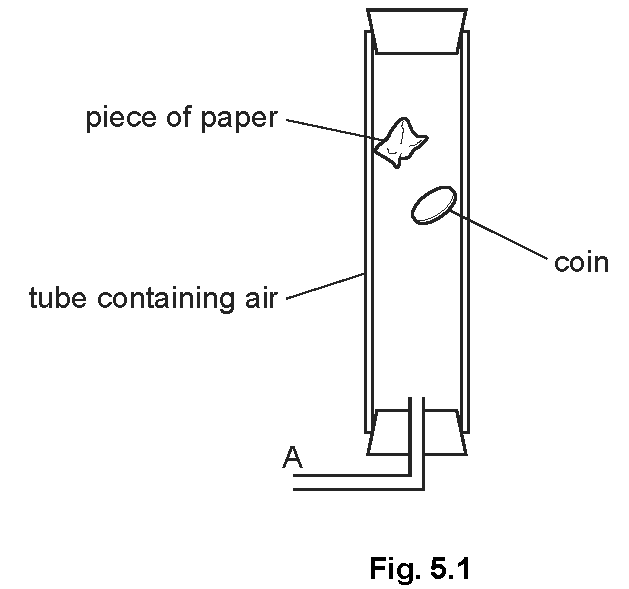 At the positions shown in Fig. 5.1, the paper is descending at constant speed but the coin still accelerates.
At the positions shown in Fig. 5.1, the paper is descending at constant speed but the coin still accelerates.
In terms of the forces acting, explain these observations.
Paper
Explanation: The forces balance out, so there is no resultant force, resulting in no acceleration.
Coin
Explanation: The downward force is larger than the upward force of air resistance, causing the coin to continue accelerating.
Question (b)
A vacuum pump is now connected at A and the air in the tube is pumped out. The paper and coin are again made to fall from rest. State one difference that would be observed, compared with what was observed when air was present.
Explanation: In the absence of air, there is no air resistance acting on the paper, so both objects fall freely under gravity.
2010 Oct-Nov Paper-42 Q1
Question (a)(i)
A hillside is covered with snow. A skier is travelling down the hill. The table below gives the values of the acceleration of the skier at various heights above the bottom of the hill.
The table below gives the values of the acceleration of the skier at various heights above the bottom of the hill.
\begin{align}
\begin{array}{|l|c|c|c|c|}
\hline \text { height } / \mathrm{m} & 350 & 250 & 150 & 50 \\
\hline \frac{\text { acceleration }}{\mathrm{m} / \mathrm{s}^2} & 7.4 & 3.6 & 1.2 & 0 \\
\hline
\end{array}
\end{align}
On Fig. 1.2, plot the values given in the table, using dots in circles. Draw the best curve for these points.
Explanation: Ensure accurate plotting and a smooth curve that best fits the plotted points.
Question (b)(i)
Describe what is happening, during the descent, to the acceleration of the skier.
Explanation: As the skier descends, the acceleration reduces due to factors such as increased friction.
Question (b)(ii)
Describe what is happening, during the descent, to the speed of the skier.
Explanation: Despite the decreasing acceleration, the skier continues to gain speed, though at a slower rate.
Question (c)
The acceleration becomes zero before the skier reaches the bottom of the hill. Use ideas about forces to suggest why this happens.
Explanation: When the forces acting on the skier balance out, there is no net force, resulting in zero acceleration.
Question (d)
Below a height of 50 m, further measurements show that the acceleration of the skier has a negative value. What does this mean is happening to the speed of the skier in the last 50 m?
Explanation: Negative acceleration indicates deceleration, meaning the skier is slowing down in the last 50 meters.
Question (e)
The skier has a mass of 60 kg. Calculate the resultant force on the skier at a height of 250 m.
Explanation: The force is calculated using \(F = ma\), where \(a = 3.6 \text{ m/s}²\). Hence, \(F = 60 \times 3.6 = 216 \text{ N}\).
2011 May-Jun Paper-41 Q1
In a laboratory, an experiment is carried out to measure the acceleration of a trolley on a horizontal table, when pulled by a horizontal force.
Fig. 1.1
 The measurements are repeated for a series of different forces, with the results shown in the table below
The measurements are repeated for a series of different forces, with the results shown in the table below
\begin{align}
\begin{array}{|l|c|c|c|c|}
\hline \text { force } / \mathrm{N} & 4.0 & 6.0 & 10.0 & 14.0 \\
\hline \frac{\text { acceleration }}{\mathrm{m} / \mathrm{s}^2} & 0.50 & 0.85 & 1.55 & 2.25 \\
\hline
\end{array}
\end{align}
(a) On Fig. 1.2, plot these points and draw the best straight line for your points.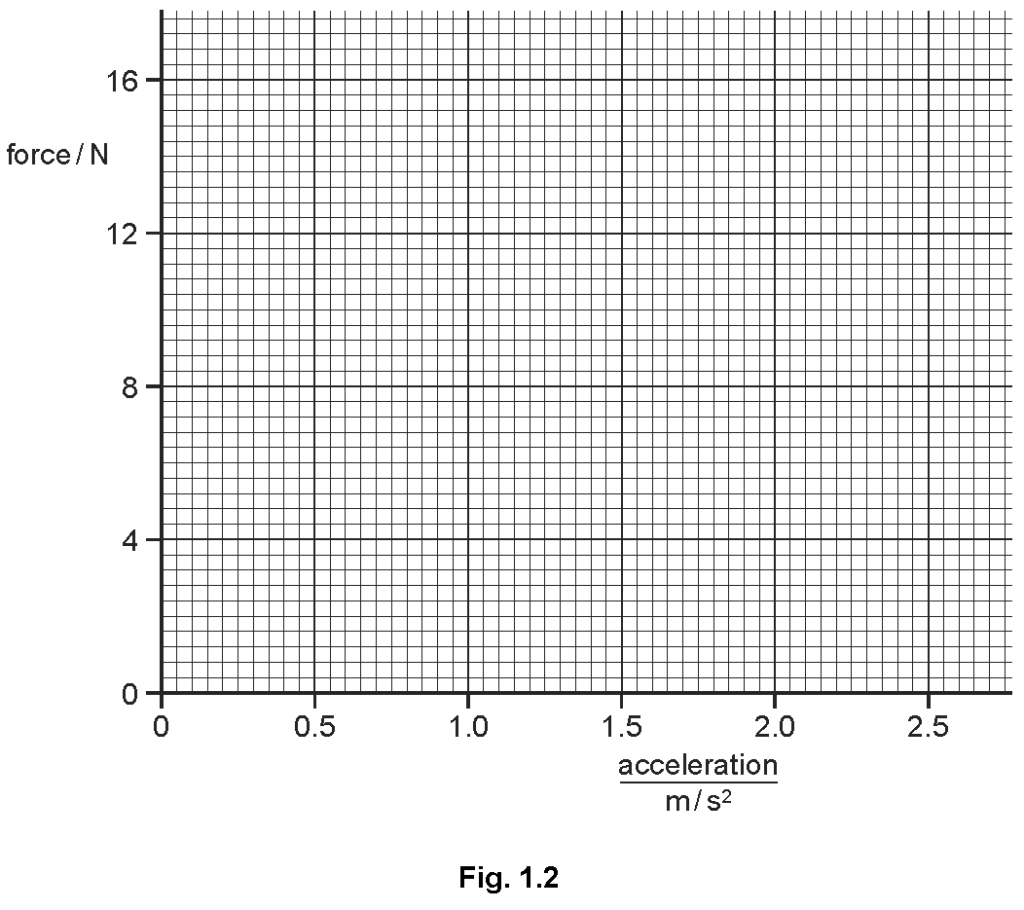
Explanation: Accurate plotting of data points and drawing a best-fit line helps visualize the relationship between variables.
(b) (i) Find the value of this force.
Explanation: This value is derived from the candidate’s correct data with unit, ensuring precision in measurements.
(ii) A force smaller than that in (b)(i) is applied to the stationary trolley. Suggest what happens to the trolley, if anything.
Explanation: A force smaller than 1.2 N is insufficient to overcome friction and initiate motion in the trolley.
(c) Show that the gradient of your graph is about 5.7.
Explanation: The gradient represents the ratio of force to acceleration, indicating the trolley's mass-related characteristics.
(d) (i) State the equation that links resultant force F, mass m and acceleration a.
Explanation: Newton's second law of motion states that the force acting on an object is equal to the mass of the object multiplied by its acceleration.
(ii) Use your gradient from (c) to find the mass of the trolley.
Explanation: By rearranging F = ma to m = F/a and using the gradient, the trolley's mass is calculated.
(e) On Fig. 1.3, sketch a speed/time graph for a trolley with constant acceleration.
Explanation: Constant acceleration results in a linear increase in speed over time, depicted as a straight line.
2011 Oct-Nov Paper-43 Q2
A person is standing on the top of a cliff, throwing stones into the sea below. (a) The person throws a stone horizontally.
(a) The person throws a stone horizontally.
(i) On Fig. 2.1, draw a line to show the path which the stone might take between leaving the person’s hand and hitting the sea.
Explanation: The stone follows a curved trajectory due to the influence of gravity, which causes it to accelerate downwards while maintaining its horizontal velocity.
(ii) On the line you have drawn, at a point halfway to the sea, mark the stone and the direction of the force on the stone.
Explanation: The only force acting on the stone in free fall (neglecting air resistance) is the force of gravity, which acts vertically downward.
(b) Later, the person drops a small stone and a large stone vertically from the edge of the cliff.
Comment on the times taken for the two stones to hit the water.
Explanation: In the absence of significant air resistance, both stones experience the same gravitational acceleration, leading to identical fall times.
(c) 800 m from the point where the person is standing, a navy ship is having target practice.
The person finds that if a stone is dropped vertically at the same time as the spurt of smoke from the ship’s gun is seen, the stone hits the water at the same time as the sound from the gun is heard.
Sound travels at 320 m/s in that region.
Calculate the velocity with which the stone hits the water.
Explanation: Using the formula \( v = at \) and given that the time is calculated as 2.5 seconds, the velocity is \( v = 10 \times 2.5 = 25 \, \text{m/s} \).
2012 Oct-Nov Paper-42 Q2
Fig. 2.1 is a head-on view of an airliner flying at constant speed in a circular horizontal path. The centre of the circle is to the left of the diagram.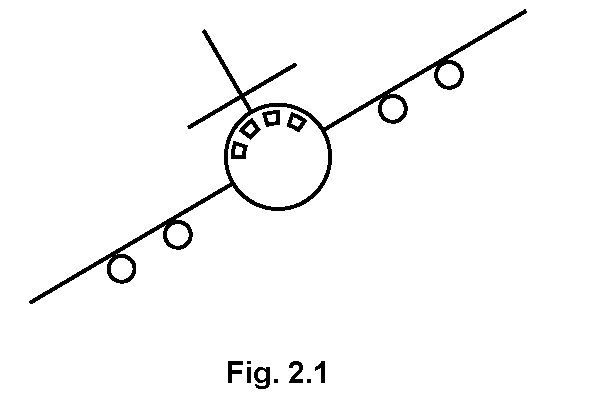 (a) On Fig. 2.1, draw the resultant force acting on the airliner. Explain your answer.
(a) On Fig. 2.1, draw the resultant force acting on the airliner. Explain your answer.
Explanation: The force that acts on the airliner is towards the center of the circular path, causing the centripetal acceleration necessary to maintain the circular motion.
(b) The weight of the airliner is 1.20 × 10⁶ N and there is an aerodynamic lift force of 1.39 × 10⁶ N acting at 30° to the left of the vertical. By drawing a scale vector diagram, or otherwise, show that the resultant of these two forces is in the same direction as the resultant force you drew in (a).

Explanation: The vector diagram shows that the sum of the weight and lift forces results in a horizontal force towards the left, aligning with the centripetal force direction.
(c) The speed is constant as the airliner flies in this circular path. State and explain what is happening to the velocity.
Explanation: Since the airliner is moving in a circular path at a constant speed, its direction continuously changes, resulting in a change in velocity.
2012 Oct-Nov Paper-43 Q1
A brick is dropped from the top of a very tall building as it is being constructed.
Fig. 1.1 is the speed/time graph for the brick as it falls to the ground.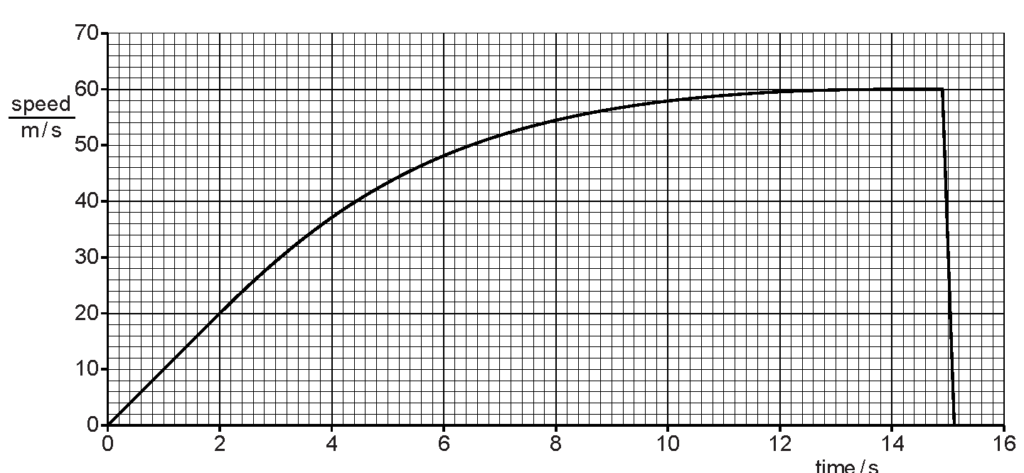 (a) State a time at which the acceleration of the brick is
(a) State a time at which the acceleration of the brick is
(i) zero,
Explanation: The brick's speed is constant during these times, indicating zero acceleration.
(ii) constant but not zero,
Explanation: The brick's speed increases linearly, indicating constant but non-zero acceleration.
(iii) not constant.
Explanation: The brick's acceleration varies as the graph shows a curve, indicating changing acceleration.
(b) Explain in terms of the forces acting on the brick why, between 0 and 14.0 s, its speed varies in the way shown by the graph.
Explanation: Gravity causes the brick to accelerate initially, but as air resistance increases, the net force decreases until it balances with gravity, resulting in terminal velocity.
(c) State the direction of the resultant force acting on the brick at time 15.0 s.
Explanation: At 15.0 s, the brick's speed decreases, indicating an upward resultant force opposing its motion.
2013 Oct-Nov Paper-42 Q2
Fig. 2.1 shows a model fire engine used by a student to take measurements of force and motion.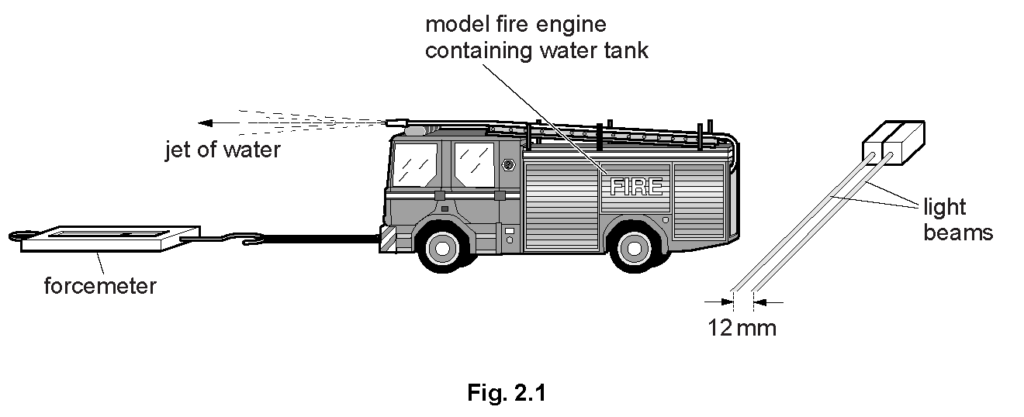 The model projects a jet of water forwards. The forcemeter holds the model stationary. It indicates a force of \(0.060 \mathrm{~N}\) acting on the model.
The model projects a jet of water forwards. The forcemeter holds the model stationary. It indicates a force of \(0.060 \mathrm{~N}\) acting on the model.
(a) The back of the model breaks a pair of light beams and the time to pass between them is measured electronically. The beams are 12 mm apart and the second beam is broken 0.080 s after the first.
The student times with a stopwatch how long it takes from the release of the model until the beams are cut.
Calculate the time he measures.
Explanation: The velocity is calculated as 0.15 m/s by dividing 12 mm by 0.080 s. The time is calculated using the equation t = (Δv)/a, which is 5.0 s after substituting the given values.
(b) This experiment is carried out with the water tank in the model nearly full.
Calculate the mass of the model including the water in the tank.
Explanation: The mass is calculated using the equation F/a = m. Substituting 0.060 N for F and 0.030 m/s² for a gives 2 kg.
(c) The student repeats the experiment with the same force but with the water tank nearly empty.
State and explain how the acceleration will compare to that of the first experiment.
Explanation: With a reduced mass and the same force, the acceleration increases according to the equation F = ma.
2014 Oct-Nov Paper-41 Q1 c
(c) Fig. 1.3 shows a person bungee-jumping from a bridge. The person is attached to a long elastic rope.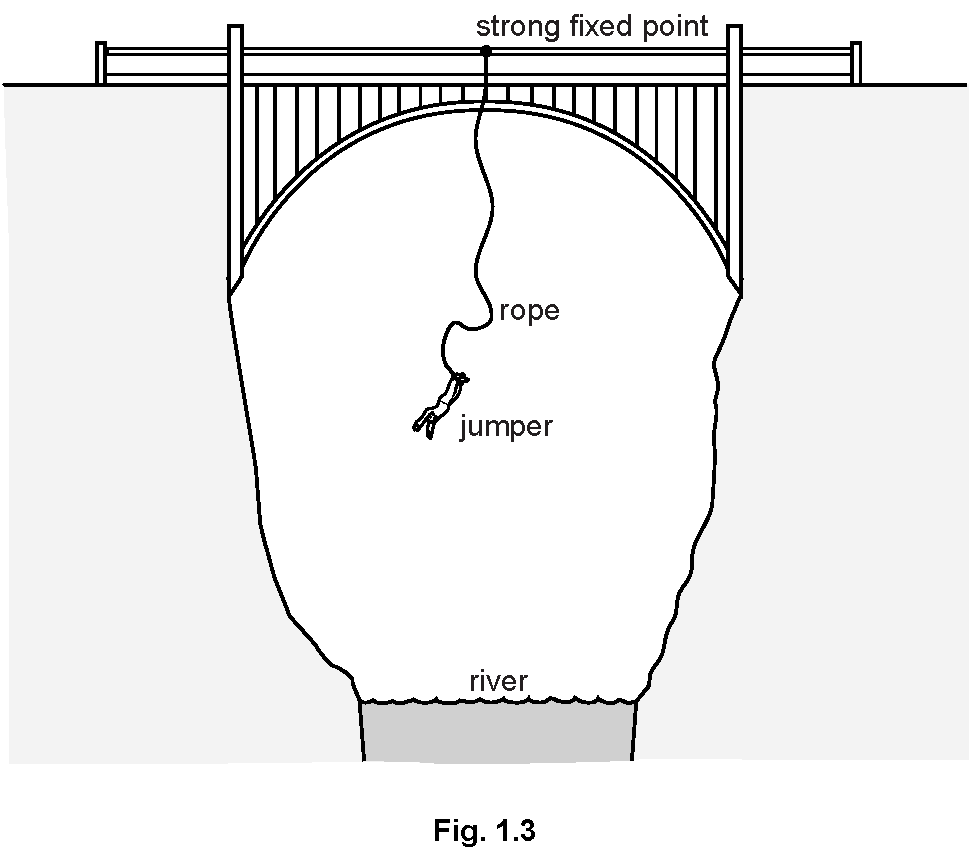 (c)(i) In 1.5 s the speed of the jumper increases from zero to 10.5 m/s. Calculate her average acceleration during this time.
(c)(i) In 1.5 s the speed of the jumper increases from zero to 10.5 m/s. Calculate her average acceleration during this time.
Explanation: The average acceleration is calculated using the formula \(a = \frac{Δv}{t}\), where \(Δv\) is the change in velocity (10.5 m/s) and \(t\) is the time (1.5 s), resulting in an acceleration of 7.0 m/s².
(c)(ii) At one point during the fall, she reaches her maximum speed. State her acceleration at this point.
Explanation: When the jumper reaches her maximum speed, her acceleration is zero because she is not speeding up or slowing down at that moment.
(c)(iii) What can be said about the forces acting on her at this point?
Explanation: At maximum speed, the forces acting on the jumper, such as gravity and the tension in the rope, balance each other, resulting in no resultant force and therefore no acceleration.
2014 Oct-Nov Paper-43 Q1
A free-fall parachutist jumps from a helium balloon, but does not open his parachute for some time.
Fig. 1.1 shows the speed-time graph for his fall. Point B indicates when he opens his parachute.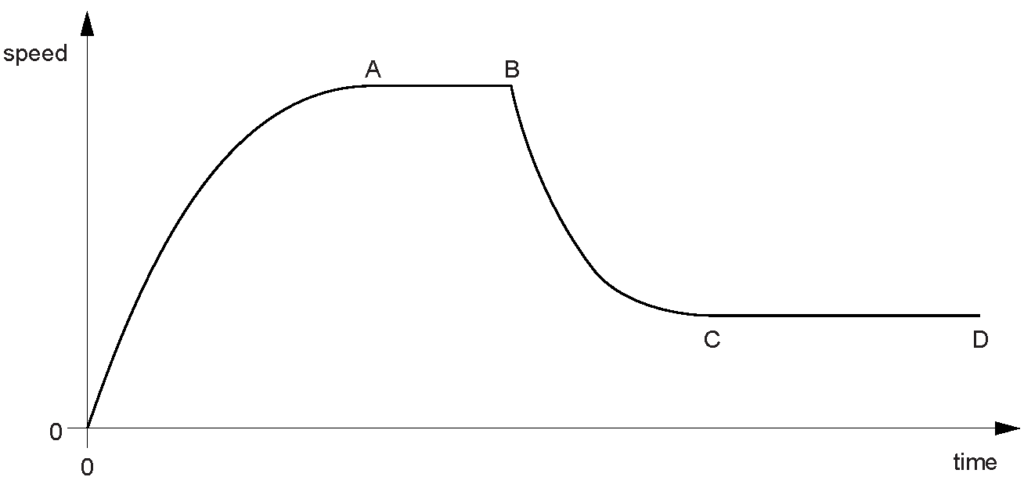 (a)(i) State the value of the gradient of the graph immediately after time t = 0.
(a)(i) State the value of the gradient of the graph immediately after time t = 0.
Explanation: This value represents the acceleration due to gravity, indicating the parachutist is in freefall immediately after the jump, accelerating at approximately 10 m/s² due to gravity.
(a)(ii) Explain why the gradient has this value.
(b) State how Fig. 1.1 shows that the acceleration decreased between time t = 0 and the time to A.
(c) Explain, in terms of forces, what is happening in section AB of the graph in Fig. 1.1.
2017 May-Jun Paper-42 Q2 a
Fig. 2.1 shows a vehicle designed to be used on the Moon.
Fig. 2.1
The brakes of the vehicle are tested on Earth.
(a) The acceleration of free fall on the Moon is one sixth \(\left(\frac{1}{6}\right)\) of its value on Earth.
Tick one box in each column of the table to predict the value of that quantity when the vehicle is used on the Moon, compared to the test on Earth.
\begin{align}
\begin{array}{|c|c|c|c|}
\hline & \begin{array}{l}
\text { mass of vehicle on } \\
\text { Moon }
\end{array} & \begin{array}{l}
\text { weight of vehicle on } \\
\text { Moon }
\end{array} & \begin{array}{l}
\text { deceleration of vehicle } \\
\text { on Moon with same } \\
\text { braking force }
\end{array} \\
\hline 10 \times \text { value on Earth } & & & \\
\hline 6 \times \text { value on Earth } & & & \\
\hline \text { same as value on Ear } & & & \\
\hline \begin{array}{l}
\frac{1}{6} \times \text { value on Earth }
\end{array} & & & \\
\hline \begin{array}{l}
\frac{1}{10} \times \text { value on Earth }
\end{array} & & & \\
\hline
\end{array}
\end{align}
– The weight of the vehicle on the Moon is 1/6th of its value on Earth.
– The deceleration of the vehicle on the Moon with the same braking force is the same as on Earth.
Explanation:– Mass is a measure of inertia and does not change with location. Thus, the mass remains the same whether on Earth or the Moon.
– Weight is a force exerted by gravity. Since the Moon's gravity is 1/6th of Earth's, the vehicle's weight is correspondingly reduced to 1/6th.
– Deceleration is influenced by the mass and the applied force. Since the mass remains constant and the braking force is the same, the deceleration does not change due to a change in gravitational acceleration alone.
2021 May-Jun Paper-42 Q3
Fig. 3.1 shows water flowing at very slow speed over a cliff edge. 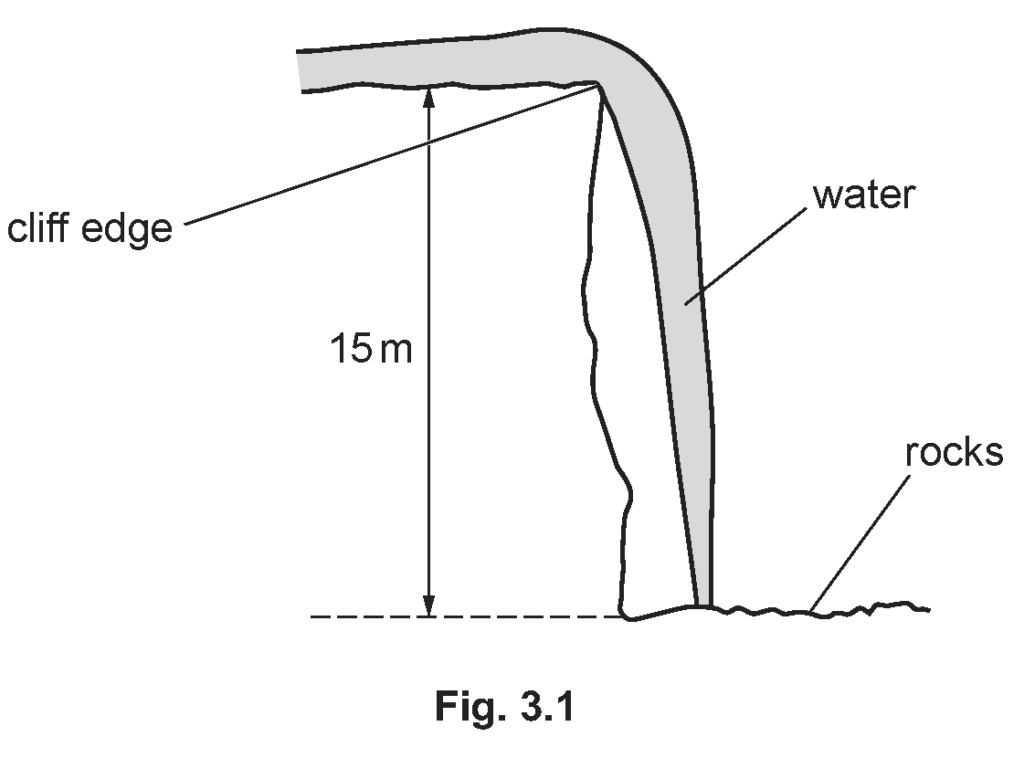 The water falls 15 m onto the rocks below.
The water falls 15 m onto the rocks below.
(a) Show that the velocity of the water when it strikes the rocks is 17 m/s.
Explanation: Using the kinematic equation \( v^2 = u^2 + 2as \), where \( u = 0 \) (initial velocity), \( a = 9.8 \) m/s² (acceleration due to gravity), and \( s = 15 \) m (distance fallen), we find \( v = \sqrt{2 \times 9.8 \times 15} = 17.15 \) m/s, which rounds to approximately 17 m/s.
(b) 30 kg of water flows over the cliff edge every second. Calculate the force exerted by the rocks on the falling water. Ignore any splashing.
Explanation: The force exerted can be calculated using the rate of change of momentum formula, \( F = \Delta p / \Delta t \). With \( \Delta p = m \times v = 30 \times 17.15 \) kg·m/s and \( \Delta t = 1 \) s, we calculate \( F = 514.5 \) N, which rounds to approximately 520 N.