Question 1
(i) Given that \(A =\left(\begin{array}{rr}4 & -3 \\ 2 & 5\end{array}\right),\) find the inverse matrix \(A ^{-1}\).
(ii) Use your answer to part (i) to solve the simultaneous equations
\[
\begin{array}{l}
4 x-3 y=-10 \\
2 x+5 y=21
\end{array}
\]
Question 2
A cuboid has a square base of side \((2+\sqrt{3}) cm\) and a volume of \((16+9 \sqrt{3}) cm ^{3}\). Without using a calculator, find the height of the cuboid in the form \((a+b \sqrt{3}) cm\), where \(a\) and \(b\) are integers.
Question 3
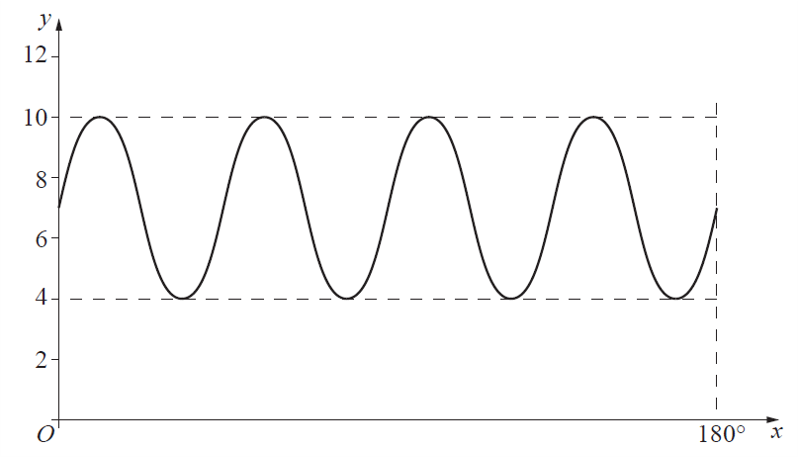
(a)The diagram shows a sketch of the curve \(y=a \sin (b x)+c\) for \(0^{\circ} \leqslant x \leqslant 180^{\circ}\). Find the values of \(a, b\) and \(c .\)
(b) Given that \(f (x)=5 \cos 3 x+1,\) for all \(x,\) state
(i) the period of \(f\),
(ii) the amplitude of \(f\).
Question 4
(i) Find \(\frac{d}{d x}\left(x^{2} \ln x\right)\)
(ii) Hence, or otherwise, find \(\int x \ln x d x\).
Question 5
(a) Solve the equation \(3^{2 x}=1000\), giving your answer to 2 decimal places.
(b) Solve the equation \(\frac{36^{2 y-5}}{6^{3 y}}=\frac{6^{2 y-1}}{216^{y+6}}\).
Question 6
By shading the Venn diagrams below, investigate whether each of the following statements is true or false. State your conclusions clearly.
(i) \(\quad A \cap B^{\prime}=\left(A^{\prime} \cap B\right)^{\prime}\)


(ii) \(\quad X \cap Y=X^{\prime} \cup Y^{\prime}\)


(iii) \(\quad(P \cap Q) \cup(Q \cap R)=Q \cap(P \cup R)\)


Question 7
Given that \(f (x)=x^{2}-\frac{648}{\sqrt{x}},\) find the value of \(x\) for which \(f ^{\prime \prime}(x)=0\)
Question 8
Relative to an origin \(O,\) the position vectors of the points \(A\) and \(B\) are \(2 i -3 j\) and \(11 i+42 j\) respectively.
(i) Write down an expression for \(\overrightarrow{A B}\).
The point \(C\) lies on \(A B\) such that \(\overrightarrow{A C}=\frac{1}{3} \overrightarrow{A B}\)
(ii) Find the length of \(\overrightarrow{O C}\).
The point \(D\) lies on \(\overrightarrow{O A}\) such that \(\overrightarrow{D C}\) is parallel to \(\overrightarrow{O B}\).
(iii) Find the position vector of \(D\).
Question 9
A particle moves in a straight line so that, \(t\) s after passing through a fixed point \(O\), its velocity, \(v ms ^{-1}\), is given by \(v=2 t-11+\frac{6}{t+1}\). Find the acceleration of the particle when it is at instantaneous rest.
Question 10
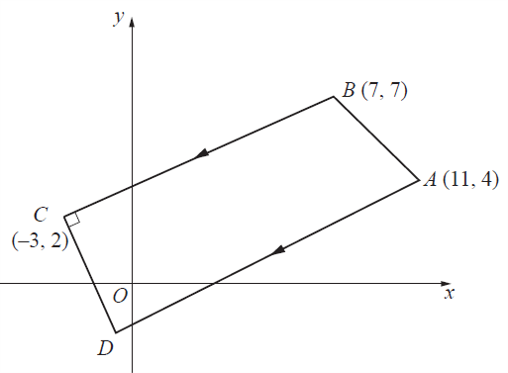
Solutions to this question by accurate drawing will not be accepted.
The diagram shows a trapezium \(A B C D\) with vertices \(A(11,4), B(7,7), C(-3,2)\) and \(D .\) The side \(A D\) is parallel to \(B C\) and the side \(C D\) is perpendicular to \(B C\). Find the area of the trapezium \(A B C D . \quad[9]\)
Question 11
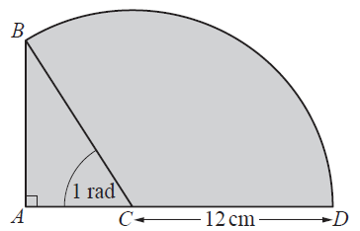
The diagram shows a right-angled triangle \(A B C\) and a sector \(C B D C\) of a circle with centre \(C\) and radius \(12 cm\). Angle \(A C B=1\) radian and \(A C D\) is a straight line.
(i) Show that the length of \(A B\) is approximately \(10.1 cm\).
(ii) Find the perimeter of the shaded region.
Question 12
Answer only one of the following two alternatives.
EITHER
The equation of a curve is \(\quad y=2 x^{2}-20 x+37\)
(i) Express \(y\) in the form \(a(x+b)^{2}+c,\) where \(a, b\) and \(c\) are integers.
(ii) Write down the coordinates of the stationary point on the curve.
A function \(f\) is defined by \(f : x \mapsto 2 x^{2}-20 x+37\) for \(x>k\). Given that the function \(f ^{-1}(x)\) exists.
(iii) write down the least possible value of \(k\),
(iv) sketch the graphs of \(y= f (x)\) and \(y= f ^{-1}(x)\) on the axes provided,
(v) obtain an expression for \(f ^{-1}\).
OR
A function g is defined by \(g : x \mapsto 5 x^{2}+p x+72,\) where \(p\) is a constant. The function can also be written as \( g : x \mapsto 5(x-4)^{2}+q\)
(i) Find the value of \(p\) and of \(q\).
(ii) Find the range of the function g.
(iii) Sketch the graph of the function on the axes provided.
(iv) Given that the function h is defined by \(h : x \mapsto \ln x,\) where \(x>0,\) solve the equation \(\operatorname{gh}(x)=12\)
