Cambridge Additional Mathematics 2011 Past Paper Oct Nov Paper 12

Question 1

Show that $\frac{1}{\tan \theta+\cot \theta}=\sin \theta \cos \theta$ . [3]

$\begin{aligned} & \frac{1}{\tan \theta+\cot \theta} \\=& \frac{1}{\left(\frac{\sin \theta}{\cos \theta}\right)+\left(\frac{\cos \theta}{\sin \theta}\right)} \\=& \frac{1}{\frac{\sin ^{2} \theta+\cos ^{2} \theta}{\sin \theta \cos \theta}} \\=& \frac{\sin \theta \cos \theta}{\sin ^{2} \theta+\cos ^{2} \theta} \\=& \sin \theta \cos \theta \text { (shown) } \end{aligned}$

Question 2

Find the coordinates of the points where the line $2 y=x-1$ meets the curve $x^{2}+y^{2}=29$ . [5]

$2 y=x-1$

$y=\frac{x-1}{2}$

Substitute into $x^{2}+y^{2}=29$

$x^{2}+\left(\frac{x-1}{2}\right)^{2}=29$
$\frac{4 x^{2}+(x-1)^{2}}{4}=29$
$4 x^{2}+x^{2}-2 x+1=116$
$5 x^{2}-2 x-115=0$
$(5 x+23)(x-5)=0$
$x=\frac{-23}{5}, x=5$

Substitute into $y=\frac{x-1}{2}$

$\begin{aligned} x &=-\frac{33}{5} \\ y &=\frac{\left(-\frac{23}{5}\right)-1}{2} \\ &=-\frac{14}{5} \\ x &=5 \\ y &=\frac{5-1}{2} \\ &=2 \end{aligned}$

The coordinate of the point are
$\left(-\frac{23}{5},-\frac{14}{5}\right)$ and (5,2)

Question 3

(i) Express $\log _{x} 2$ in terms of a logarithm to base 2. [1]

$\log _{x} 2$

$=\frac{\log _{2} 2}{\log _{2} x}$

$=\frac{1}{\log _{2} x}$

(ii) Using the result of part (i), and the substitution $u=\log _{2} x$ , find the values of $x$ which satisfy the equation $\log _{2} x=3-2 \log _{x} 2$ [4]

$\log _{2} x=3-2 \log _{2} 2$

$\log _{2} x=3-2\left(\frac{1}{\log _{2} x}\right)$

Substitute $u=\log _{2} x$

$u=3-\frac{2}{u}$
$u-3=-\frac{2}{u}$
$u^{2}-3 u=-2$
$u^{2}-3 x+2=0$
$(u-1)(u-2)=0$
$u=1, u=2$

$\begin{aligned} \log _{2} x_{1} &=1 \\ x_{1} &=2 \end{aligned}$

$\log _{2} x_{2}=2$
$x_{2}=4$

Question 4

A curve has equation $y=\left(3 x^{2}+15\right)^{\frac{2}{3}}$ . Find the equation of the normal to the curve at the point where $x=2$ . [6]

when

$x=2,$

$y=\left(3(2)^{2}+15\right)^{\frac{2}{3}}$

$y=9$

$\frac{d y}{d x}=\frac{2}{3}\left(3 x^{2}+15\right)^{-\frac{1}{3}}(6 x)$
$\frac{d y}{d x}=4 x\left(3 x^{2}+15\right)^{-\frac{1}{3}}$

$\begin{aligned} & \text { When } x=2, \\ \frac{d y}{d x} &=4(2)\left(3(2)^{2}+(15)\right)^{-\frac{1}{3}}.\\ &=\frac{8}{\sqrt[3]{(12+(15)}} \\ &=\frac{8}{\sqrt[3]{27}} \\ &=\frac{8}{3} \end{aligned}$

Gradient of the normal
$m=-\frac{3}{8}$

Equation of the normal
$\begin{aligned} y-9 &=-\frac{3}{8}(x-2) \\ y-9 &=-\frac{3}{8} x+\frac{3}{4} \\ y &=\frac{39}{4}-\frac{3}{8} x \end{aligned}$

Question 5

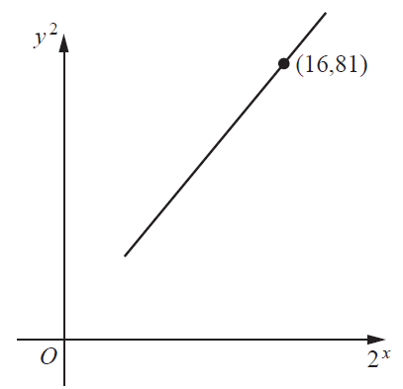
Variables $x$ and $y$ are such that, when $y^{2}$ is plotted against $2^{x}$ , a straight line graph is obtained. This line has a gradient of 5 and passes through the point (16,81) .

(i) Express $y^{2}$ in terms of $2^{x}$ . [6]

$Y=m X+C$

$At (16,81)$

$81=5(16)+c$

$c=1$

$Y=y^{2}$
$X=2^{x}$
$m=5$
$c=1$
Therefore
$y^{2}=5\left(2^{2}\right)+1$

(ii) Find the value of x when y = 6. [3]

$y^{2}=5\left(2^{x}\right)+1$

$(6)^{2}=5\left(2^{x}\right)+1$

$5\left(2^{x}\right)=36-1$

$2^{x}=\frac{35}{5}=7$

$\lg 2^{x}=\lg 7$

$x=\frac{\lg 7}{\lg 2}=2.81$

Question 6

(i) Given that $(3+x)^{5}+(3-x)^{5}=A+B x^{2}+C x^{4},$ find the value of $A,$ of $B$ and of $C$ . [4]

(ii) Hence, using the substitution $y=x^{2},$ solve, for $x,$ the equation $(3+x)^{5}+(3-x)^{5}=1086$ . [4]

Available soon

Question 7

(i) Show that $\frac{(4-\sqrt{x})^{2}}{\sqrt{x}}$ can be written in the form $p x^{-\frac{1}{2}}+q+r x^{\frac{1}{2}},$ where $p, q$ and $r$ are integers to be found. [3]

Available soon

(ii) A curve is such that $\frac{ d y}{ d x}=\frac{(4-\sqrt{x})^{2}}{\sqrt{x}}$ for $x>0$ . Given that the curve passes through the point (9,30) , find the equation of the curve. [5]

Available soon

Question 8

The line $C D$ is the perpendicular bisector of the line joining the point $A(-1,-5)$ and the point $B(5,3)$

(i) Find the equation of the line $C D$ . [4]

$\begin{aligned} \operatorname{Mid}_{A B} &=\left(\frac{5-1}{2}, \frac{3-5}{2}\right) \\ &=(2,-1) \end{aligned}$

$\begin{array}{l} m_{A B}=\frac{3+5}{5+1} \\ m_{A B}=\frac{4}{3} \end{array}$

$\begin{aligned} m_{A B} \times & m_{C D}=-1 \\ & m_{C D}=-\frac{3}{4} \end{aligned}$

$\begin{aligned} y+1 &=-\frac{3}{4}(x-2) \\ y &=-\frac{3}{4} x+\frac{1}{2} \end{aligned}$

(ii) Given that $M$ is the midpoint of $A B$ , that $2 C M=M D$ , and that the $x$ -coordinate of $C$ is -2 , find the coordinates of $D .$ [3]

$M(2,-1), C\left(-2, y_{c}\right), D\left(x_{d}, y_{d}\right)$

Equation of line $C D$
$y=-\frac{3}{4} x+\frac{1}{2}$

$A+C\left(-2, y_{c}\right)$
$y_{c}=-\frac{3}{4}(-2)+\frac{1}{2}=2$

$\left(\frac{(1) x_{d}+2(-2)}{1+2}, \frac{(1) y_{d}+2(2)}{1+2}\right)=(2,-1)$

$\frac{x_{d}-4}{3}=2$
$x_{d}=10$

$\frac{y_{d} +2(2)}{3}=-1$
$y_{d}=-7$

(iii) Find the area of the triangle $C A D$ . [2]

$A=\frac{1}{2}\left|\begin{array}{cccc}-2 & -1 & 10 & -2 \\ 2 & -5 & -7 & 2\end{array}\right|$

$A=\frac{1}{2}|10+7+20+2+50-14|$

$A=\frac{1}{2}|75|$

$A=37.5$ unit

$^{2}$

Question 9

(i) Given that $y=x \sin 4 x,$ find $\frac{ d y}{ d x}$ . [3]

$\begin{aligned} y &=x \sin 4 x \\ \frac{d y}{d x} &=(1) \sin 4 x+\cos 4 x(4) x \\ &=\sin 4 x+4 x \cos 4 x \end{aligned}$

(ii) Hence find $\int x \cos 4 x d x$ and evaluate $\int_{0}^{\frac{\pi}{8}} x \cos 4 x d x$ . [6]

$\frac{d}{d x} x \sin 4 x=4 x \cos 4 x+\sin 4 x$

$\int(4 x \cos 4 x+\sin 4 x) d x=x \sin 4 x$

$\int 4 x \cos 4 x+\int \sin 4 x d x=x \sin 4 x$

$4 \int x \cos 4 x=x \sin 4 x-\int \sin 4 x d x$

$\int x \cos 4 x=\frac{1}{4} x \sin 4 x-\frac{1}{4}\left[-\frac{\cos 4 x}{4}\right]+c$

$=\frac{1}{4} x \sin 4 x+\frac{1}{16} \cos 4 x+c$

$\begin{aligned} & \int_{0}^{\frac{\pi}{8}} x \cos 4 x d x \\=&\left[\frac{1}{4} x \sin 4 x+\frac{1}{16} \cos 4 x\right]_{0}^{\frac{\pi}{8}} \\=&\left[\frac{1}{4}\left(\frac{\pi}{8}\right) \sin 4\left(\frac{\pi}{8}\right)+\frac{1}{16} \cos 4\left(\frac{\pi}{8}\right)\right]-\left[0+\frac{1}{16} \cos 0\right] \\=&\left[\frac{\pi}{32}(1)+0\right]-\frac{1}{16} \\=& \frac{\pi}{32}-\frac{1}{16} \end{aligned}$

Question 10

(i) Solve $2 \sec ^{2} x=5 \tan x+5,$ for $0^{\circ}<x<360^{\circ}$ . [5]

$2 \sec ^{2} x=5 \tan x+5$

$2\left(\tan ^{2} x+1\right)=5 \tan x+5$

$2 \tan ^{2} x+2=5 \tan x+5$

$2 \tan ^{2} x-5 \tan x-3=0$

$\tan x=y$
$2 y^{2}-5 y-3=0$
$(2 y+1)(y-3)=0$
$y=-\frac{1}{2}, y=3$

$\begin{aligned} \tan & x=-\frac{1}{2} \\ x &=180^{\circ}-26.57^{\circ} \\ &=153.43^{\circ} \end{aligned}$
or
$\begin{aligned} x &=360^{\circ}-26 \cdot 57^{\circ} \\ &=333.43^{\circ} \end{aligned}$

$\begin{aligned} \tan x &=3 \\ x &=71.57^{\circ} \end{aligned}$
or
$\begin{aligned} x &=180^{\circ}+71.57^{\circ} \\ &=251.57^{\circ} \end{aligned}$

(ii) Solve $\sqrt{2} \sin \left(\frac{y}{2}+\frac{\pi}{3}\right)=1,$ for $0<y<4 \pi$ radians. [5]

$0<y<4 \pi$

$0<\frac{y}{2}<2 \pi$

$\frac{\pi}{3}<\frac{y}{2}+\frac{\pi}{3}<2 \frac{1}{3} \pi$

$\sqrt{2} \sin \left(\frac{y}{2}+\frac{\pi}{3}\right)=1$
$\sin \left(\frac{y}{2}+\frac{\pi}{3}\right)=\frac{1}{\sqrt{2}}$

$\frac{y}{2}+\frac{\pi}{3}=\pi-\frac{\pi}{4}$
$\frac{y}{2}=\frac{3 \pi}{4}-\frac{\pi}{3}$
$\frac{y}{2}=\frac{5 \pi}{12}$
$y=\frac{5 \pi}{6}$
or
$\frac{y}{2}+\frac{\pi}{3}=2 \pi+\frac{\pi}{4}$
$\frac{y}{2}=\frac{9 \pi}{4}-\frac{\pi}{3}$
$y=\frac{23 \pi}{6}$

Question 11

Answer only one of the following two alternatives.
EITHER
A curve has equation $y= e ^{-x}(A \cos 2 x+B \sin 2 x)$ . At the point (0,4) on the curve, the gradient of the tangent is 6

(i) Find the value of $A$ . [1]

Available soon

(ii) Show that $B=5$ . [5]

Available soon

(iii) Find the value of $x$ , where $0<x<\frac{\pi}{2}$ radians, for which $y$ has a stationary value. [5]

Available soon

A curve has equation $y=\frac{\ln \left(x^{2}-1\right)}{x^{2}-1},$ for $x>1$ .

(i) Show that $\frac{ d y}{ d x}=\frac{k x\left(1-\ln \left(x^{2}-1\right)\right)}{\left(x^{2}-1\right)^{2}},$ where $k$ is a constant to be found. [4]

Available soon

(ii) Hence find the approximate change in $y$ when $x$ increases from $\sqrt{5}$ to $\sqrt{5}+p$ , where $p$ is small. [2]

Available soon

(iii) Find, in terms of e, the coordinates of the stationary point on the curve. [5]

Available soon

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Question 9

Question 10

Question 11

Leave a Comment Cancel reply