As discussed, the spring constant (k) is specific to a particular spring or wire and doesn’t account for the material’s inherent properties. To compare the stiffness of different materials, the Young modulus is used.
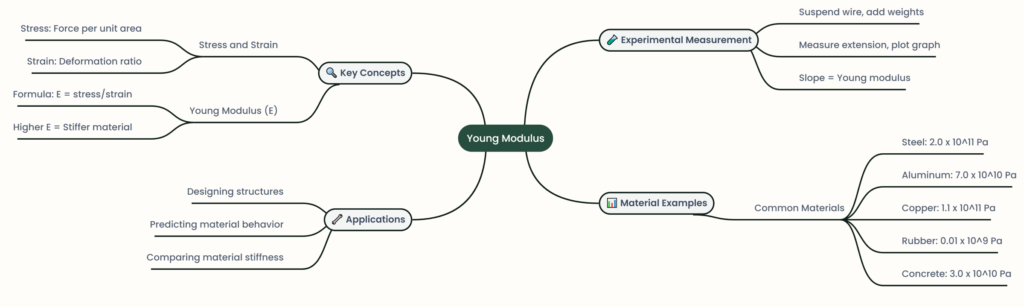
Defining Stress and Strain
Imagine applying a force to a wire – it causes a deformation or change in length. This deformation is quantified by strain, which measures the extent of deformation relative to the object’s original size. For a wire of original length Lo extended by an amount e, the tensile strain (ε) is calculated as follows:
$$\text{strain} = \frac{\text{extension}}{\text{original length}}$$
$$\varepsilon = \frac{e}{L_o}$$
Note: Strain is a ratio of lengths and therefore has no unit.
Strain is caused by stress, which is the force acting over a given area. In the case of stretching or compressing a wire, we consider tensile stress, defined as the force acting perpendicularly to a cross-sectional area:
$$\text{stress} = \frac{\text{force}}{\text{area normal to the force}}$$
$$\sigma = \frac{F}{A}$$
Tensile stress is measured in Newtons per square meter (N m-2) or Pascals (Pa), the same unit used for pressure.
The Young Modulus: Connecting Stress and Strain
Within the limit of proportionality, the relationship between stress and strain is directly proportional. This means that doubling the stress will double the strain. This proportionality is represented by the Young modulus (E), a material property that quantifies stiffness:
$$\text{stress} \propto \text{strain}$$
$$\text{stress} = E \times \text{strain}$$
$$E = \frac{\text{stress}}{\text{strain}}$$
$$E = \frac{\sigma}{\varepsilon}$$
Substituting the expressions for stress and strain, we get:
$$E = \frac{(F / A) \cdot L_o}{e} = \frac{F \cdot L_o}{A \cdot e}$$
The Young modulus is measured in the same unit as stress, Pascals (Pa) or N m-2, because strain has no unit. A higher Young modulus indicates a stiffer material, meaning it requires a greater stress to produce the same strain.
Measuring the Young Modulus Experimentally
The Young modulus of a metal wire can be determined experimentally by applying loads, measuring the resulting extensions, and knowing the wire’s original length and cross-sectional area. A common experimental setup involves a long wire suspended vertically with a weight attached to its free end.
Here’s a breakdown of the experimental procedure:
- A long wire (often copper) is clamped at one end and allowed to hang vertically.
- A reference mark is attached to the wire a known distance (Lo) from the clamp.
- The diameter (d) of the wire is measured using a micrometer screw gauge. The cross-sectional area (A) is then calculated using:
$$A = \frac{\pi d^2}{4}$$ - Weights of known mass (m) are added to the wire’s free end, creating a load (F) calculated as:
$$F = mg$$ - The extension (e) caused by each load is measured.
- A graph of force (F) against extension (e) is plotted. The gradient of this graph is equal to:
$$\frac{E \cdot A}{L_o}$$ - The Young modulus (E) is calculated using:
$$E = \frac{\text{gradient} \cdot L_o}{A}$$
Important Note: The experiment must be conducted within the elastic limit of the wire, ensuring that the wire returns to its original length after removing the loads.
Significance of the Young Modulus
The Young modulus is a crucial material property used in various engineering applications. For example:
- Designing structures: Engineers use the Young modulus to select materials that can withstand specific loads without excessive deformation.
- Predicting material behavior: The Young modulus helps predict how a material will behave under different stress conditions.
- Comparing material stiffness: The Young modulus allows for the comparison of the stiffness of various materials, aiding in material selection for specific applications.
Table below lists the Young modulus values for various materials, showcasing the vast range of stiffness exhibited by different substances.
| Material | Young Modulus (Pa) |
|---|---|
| Steel | 2.0 × 1011 |
| Aluminum | 7.0 × 1010 |
| Copper | 1.1 × 1011 |
| Rubber | 0.01 × 109 |
| Concrete | 3.0 × 1010 |