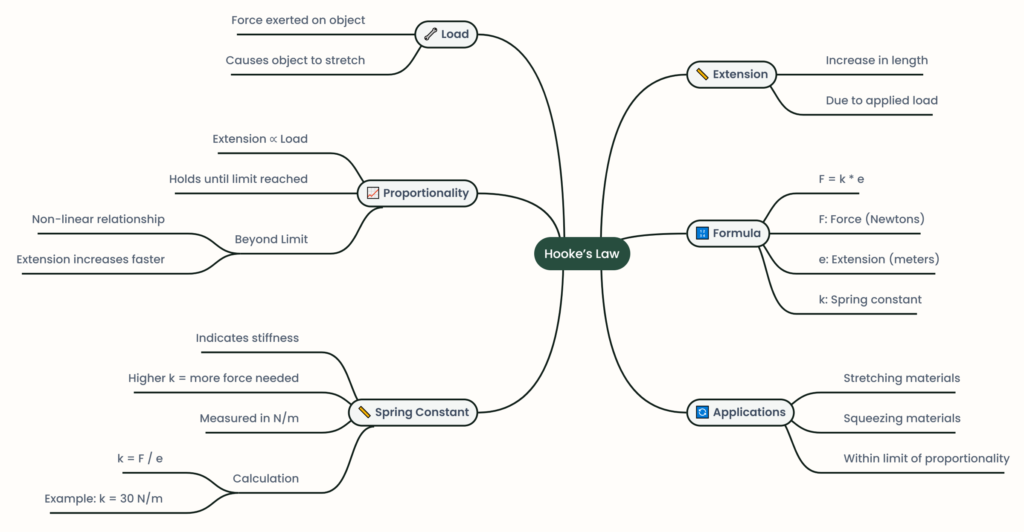
Key Concepts:
- Load: The tensile force exerted on an object, such as a spring or wire, which causes it to stretch or extend.
- Extension: The increase in an object’s length or deformation from its original state when subjected to a load.
As the load applied to an object increases, the extension also increases. Initially, this relationship is
directly proportional—if the load doubles, the extension doubles as well. This proportionality holds
only up to the limit of proportionality. Beyond this point, the extension grows faster than the load, and
the relationship becomes non-linear.
The Principle of Hooke’s Law:
Hooke’s Law describes the proportional relationship between the force applied to an object and its extension,
provided the limit of proportionality is not exceeded. It can be expressed mathematically as:
\[
F \propto e
\]
Introducing a constant converts the proportionality into an equation:
\[
F = k \cdot e
\]
Where:
- \( F \): The applied force or load (in Newtons, \( \text{N} \)).
- \( e \): The extension (in meters, \( \text{m} \)).
- \( k \): The spring constant or force constant, representing the object’s stiffness.
A higher spring constant indicates greater stiffness, meaning more force is needed for the same extension.
The spring constant, \( k \), is measured in Newtons per meter (\( \text{N/m} \)) and can be calculated using:
\[
k = \frac{F}{x}
\]
Where:
- \( F \): The applied force.
- \( x \): The extension.
Applications:
Hooke’s Law applies to both extension (stretching) and compression (squeezing).
In compression, the compression is calculated as the difference between the original length
and the reduced length. This law is valid as long as the object remains within its limit of proportionality.
Worked Examples:
Example 1:
An elastic cord originally 10 cm long is stretched to 15 cm by a 1.50 N force applied at both ends.
Calculate the force constant of the cord.
Solution:
\[
\text{Extension} = 15 \, \text{cm} – 10 \, \text{cm} = 5 \, \text{cm} = 0.05 \, \text{m}
\]
\[
k = \frac{F}{e} = \frac{1.5 \, \text{N}}{0.05 \, \text{m}} = 30 \, \text{N/m}
\]
These examples illustrate the practical application of Hooke’s Law in calculating the spring constant
for objects experiencing either extension or compression.